relacion matematica

"relación matemática"

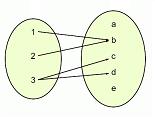
Una relación es un vínculo o una correspondencia. En el caso de larelación matemática, se trata de la correspondencia que existe entre dos conjuntos: a cada elemento del primer conjunto le corresponde al menos un elemento del segundo conjunto.

Cuando a cada elemento de un conjunto le corresponde solo uno del otro, se habla de función. Esto quiere decir que las funciones matemáticas siempre son, a su vez, relaciones matemáticas, pero que las relaciones no siempre son funciones.

En una relación matemática, al primer conjunto se lo conoce como dominio, mientras que el segundo conjunto recibe el nombre de rango o recorrido. Las relaciones matemáticas existentes entre ellos se pueden graficar en el esquema llamado plano cartesiano.

Supongamos que el dominio se llama M y el rango, N. Una relación matemática deM en N será un subconjunto del producto cartesiano M x N. Las relaciones, en otras palabras, serán pares ordenados que vinculen elementos de M con elementos de N.

Si M = {5, 7} y N = {3, 6, 8}, el producto cartesiano de M x N serán los siguientes pares ordenados:

M x N = {(5, 3), (5, 6), (5, 8), (7, 3), (7, 6), (7, 8)}

Con este producto cartesiano, se pueden definir diferentes relaciones. La relación matemática del conjunto de pares cuyo segundo elemento es menor a 7 es R = {(5, 3), (5, 6), (7, 3), (7, 6)}

Otra relación matemática que puede definirse es aquella del conjunto de pares cuyo segundo elemento es par: R = {(5, 6), (5, 8), (7, 6), (7, 8)}

"relación matemática"

Una relación ${\displaystyle R_{\ }^{\ }}$, de los conjuntos ${\displaystyle A_{1},A_{2},\ldots ,A_{n}}$ es un subconjunto del producto cartesiano

${\displaystyle R\subseteq A_{1}\times A_{2}\times \ldots \times A_{n}}$

Una relación binaria es una relación entre dos conjuntos.

El concepto de relación implica la idea de enumeración, de algunos de los elementos, de los conjuntos que forman tuplas.

${\displaystyle R(a_{1},a_{2},\ldots ,a_{n})\qquad {\mbox{o bien}}\qquad (a_{1},a_{2},\ldots ,a_{n})\in R}$

Un caso particular es cuando todos los conjuntos de la relación son iguales: ${\displaystyle A_{1}=A_{2}=\ldots =A_{n}}$ en este caso se representa ${\displaystyle A\times A\times \ldots \times A}$ como ${\displaystyle A^{n}\,}$, pudiéndose decir que la relación pertenece a A a la n.

${\displaystyle R\subseteq A^{n}}$

"relación matemática"

DEFINICIÓN MATEMÁTICA DE RELACIÓN Y DE FUNCIÓN
En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito).

Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.

De las definiciones anteriores podemos deducir que todas las funciones son relaciones, pero no todas las relaciones son funciones.

DEFINICIÓN MATEMÁTICA DE RELACIÓN Y DE FUNCIÓN
TUTORIAL DE REFUERZO.

Operación unaria

Ir a la navegaciónIr a la búsqueda

Se define como operación unaria aquella operación matemática, que sólo necesita el operador y un único operando (argumento) para que se pueda calcular un valor.

Por ejemplo, la función valor absoluto «| |» es un operador unario, porque sólo necesita un argumento.

También podemos ver que: dado un conjunto A, el complemento de un elemento a de A es otro elemento b de A, definiendo a b como el complemento de a:

${\displaystyle {\begin{array}{rccl}\sim :&A&\longrightarrow &A\\&a&\longmapsto &b=\sim a\end{array}}}$

Con lo que tenemos que el complemento es una operación unaria interna, si a cada elemento a de A le corresponde un único elemento b de A, siendo b el complemento de a.

Qué es Binario: 

Binario es un término para hacer referencia que alguna cosa está compuesta por 2 elementos o 2 unidades, ya que el prefijo "Bi" proviene del número 2. El origen etimológico de la palabra Binario proviene del latín “binarius” que significa “algo que comprende 2 unidades o elementos”, esto debido a la traducción que conlleva dicha palabra compuesta, la primera parte referida al “Bini” quiere decir o equivale a “de 2 en 2”, y el segundo vocablo que es el sufijo “ario” que se traduce como “relativo a algo”, por lo tanto, tenemos que binario quiere decir algo que se refiere a una cosa o sistema que va de 2 en 2.

Relación ternaria

Ir a la navegaciónIr a la búsqueda

En matemáticas, una relación ternaria R es el conjunto de ternas, ${\displaystyle (a,b,c)\in A\times B\times C}$ que cumplen una determinada condición que define R

${\displaystyle R=\{(a,b,c):\;a\in A\land b\in B\land c\in C\land R(a,b,c)=cierto\}}$