concepto de conjuntos

"Concepto de conjuntos"

Se denomina conjunto a la agrupación de entes o elementos, que poseen una o varias características en común. Es un concepto intuitivo empleado en matemática, que elaboró la teoría de conjuntos. Para saber si un conjunto está bien definido habrá que atender a la siguiente regla: cuando la pertenencia de un elemento a un conjunto es clara, el conjunto estará bien definido. Por ejemplo, nadie dudaría de incluir al Domingo entre los días de la semana, pero el conjunto de personas rubias no está bien definido, pues hay dudas si determinadas personas pertenecen o no al conjunto, pues la calidad de rubio no es precisa.

"Subconjuntos"

Conjunto de elementos que tienen las mismas características y que está incluido dentro de otro conjunto más amplio.

el conjunto de los números pares es un subconjunto del conjunto de los números enteros

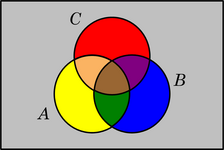
"Diagramas de venn"

Los diagramas de Venn son esquemas usados en la teoría de conjuntos, tema de interés en matemáticas, lógica de clases y razonamiento diagramático. Estos diagramas muestran colecciones (conjuntos) de cosas (elementos) por medio de líneas cerradas. La línea cerrada exterior abarca a todos los elementos bajo consideración, el conjunto universal U.

"Operaciones y leyes de conjuntos"

Union A>>B :En la teoría de conjuntos, la unión de dos (o más) conjuntos es una operación que resulta en otro conjunto, cuyos elementos son los mismos de los conjuntos iniciales. Por ejemplo, el conjunto de los números naturales es la unión del conjunto de los números pares positivos P y el conjunto de los números impares positivos I:

${\displaystyle P=\{2,4,6,\ldots \}}$

${\displaystyle I=\{1,3,5,\ldots \}}$

${\displaystyle \mathbb {N} =\{1,2,3,4,\ldots \}}$

La Ley Distributiva expresa que se obtiene la misma respuesta cuando multiplicas un conjunto de números por otro número que cuando se hace cada multiplicación por separado.

Ejemplo: (2 + 4) × 5 = 2×5 + 4×5.
Como se puede ver al realizar los cálculos 6 × 5 = 30 y 10 + 20 = 30.Entonces, el "2+4" puede ser "distribuido" entre los "por 5" en 2 por 5 y 4 por 5. 

El complemento a dos de un número N que, expresado en el sistema binario está compuesto por n dígitos, se define como:

${\displaystyle C_{2}^{N}=2^{n}-N}$

El total de números positivos será ${\displaystyle 2^{n-1}-1}$ y el de negativos ${\displaystyle 2^{n-1}}$, siendo n el número máximo de bits. El 0 contaría aparte.

Veamos un ejemplo: tomemos el número ${\displaystyle N=45}$ que, cuando se expresa en binario es ${\displaystyle N=101101_{2}}$, con 6 dígitos, y calculemos su complemento a dos:

${\displaystyle N=45}$, ${\displaystyle n=6}$; ${\displaystyle 2^{6}=64}$ y, por lo tanto: ${\displaystyle C_{2}^{N}=64-45=010011_{2}}$

Puede parecer farragoso, pero es muy fácil obtener el complemento a dos de un número a partir de su complemento a uno, porque el complemento a dos de un número binario es una unidad mayor que su complemento a uno, es decir:

${\displaystyle C_{2}^{N}=C_{1}^{N}+1}$

Cabe señalar que en este ejemplo se ha limitado el número de bits a 6, por lo que no sería posible distinguir entre el -45 y el 19 (el 19 en binario es 10011). En realidad, un número en complemento a dos se expresa con una cantidad arbitraria de unos a la izquierda, de la misma manera que un número binario positivo se expresa con una cantidad arbitraria de ceros. Así, el -45, expresado en complemento a dos usando 8 bits sería 11010011, mientras que el 19 sería 00010011; y expresados en 16 bits serían 1111111111010011 y 0000000000010011 respectivamente. Se presenta la tabla de verdad del complemento a 2 para cuatro dígitos.

En lógica proposicional y álgebra de Boole, las leyes de De Morgan¹​²​³​ son un par de reglas de transformación que son ambas reglas de inferencia válidas. Las normas permiten la expresión de las conjunciones y disyunciones puramente en términos de vía negación.

Las reglas se pueden expresar en español como:

La negación de la conjunción es la disyunción de las negaciones.
La negación de la disyunción es la conjunción de las negaciones.

o informalmente como:

"no (A y B)" es lo mismo que "(no A) o (no B)"

y también,

"no (A o B)" es lo mismo que "(no A) y (no B)"

Las reglas pueden ser expresadas en un lenguaje formal con dos proposiciones P y Q, de esta forma:

${\displaystyle \neg (P\land Q)\iff (\neg P)\lor (\neg Q)}$

${\displaystyle \neg (P\lor Q)\iff (\neg P)\land (\neg Q)}$

donde:

• ¬ es el operador de negación (NO)
• ${\displaystyle \land }$ es el operador de conjunción (Y)
• ${\displaystyle \lor }$ es el operador de disyunción (O)
• ⇔ es un símbolo metalógico que significa "puede ser reemplazado en una prueba lógica"

En teoría de conjuntos, la diferencia simétrica de dos conjuntos es una operación que resulta en otro conjunto cuyos elementos son aquellos que pertenecen a alguno de los conjuntos iniciales, sin pertenecer a ambos a la vez. Por ejemplo, la diferencia simétrica del conjunto de los números pares P y el conjunto de los cuadrados perfectos C es un conjunto D que contiene los cuadrados impares y los pares no cuadrados:

${\displaystyle P=\{2,4,6,8,10,12,14,16,\ldots \}}$

${\displaystyle C=\{1,4,9,16,25,\ldots \}}$

${\displaystyle D=\{1,2,6,8,9,10,12,14,18,\ldots \}}$

La diferencia simétrica de conjuntos se denota por Δ, por lo que P Δ C = D.

Simplificación de Expresiones:

La simplificación de expresiones consiste en agrupar los términos semejantes y simplificarlo, si es posible.
Para simplificar la expresión se suman o restan los coeficientes de los términos semejantes.
Por ejemplo:    4a - 3b + 2a
4a y 2a son términos semejantes
-3b   no es término semejante
4a + 2a - 3b   ( Se agrupan los términos semejantes)
6a - 3b           ( Se resuelve la expresión)
Ejemplo:
2a + 4c
La expresión no se puede simplificar, ya que 2a y 4c no son términos  semejantes .  Entonces, la expresión ya está simplificada.
Otro ejemplo:
3x + 2y - 9 + 4x +6
3x, 4x son términos semejantes
2y
-9, 6 son términos semejantes
Reagrupar términos semejantes:
3x + 4x  + 2y  -  9 + 6
7x  + 2y - 3
Ejemplo:
2xy + 4z -9 + 2y _ xy
2xy y 2y No son términos semejantes.  Para ser términos semejantes, deben tener exactamente las mismas variables con los mismos exponentes.
2xy, -xy           son términos semejantes
4z
9x
2y
2xy - xy + 4z - 9x+ 2y
      xy + 4z - 9x + 2y

Dado un conjunto ${\displaystyle {\mathfrak {B}}}$ en el que se han definido dos leyes de composición interna ${\displaystyle \oplus ,\odot }$. La estructura ${\displaystyle ({\mathfrak {B}},\oplus ,\odot )}$ es un álgebra de Boole si y solo si ${\displaystyle ({\mathfrak {B}},\oplus ,\odot )}$ es un Retículo distributivo,⁵​ esto es:

• ${\displaystyle \odot }$ es distributiva respecto a ${\displaystyle \oplus }$:

${\displaystyle a\odot (b\oplus c)=(a\odot b)\oplus (a\odot c)}$

• ${\displaystyle \oplus }$ es distributiva respecto a ${\displaystyle \odot }$

${\displaystyle a\oplus (b\odot c)=(a\oplus b)\odot (a\oplus c)}$

Basándose en esta definición se determina lo siguiente.

En matemáticas, un conjunto finito es un conjunto que tiene un número finito de elementos. Por ejemplo {2, 4, 6, 8, 10} es un conjunto finito con cinco elementos. La cardinalidad o número de elementos de un conjunto finito es igual a un número natural.

Si un conjunto no es finito, entonces es infinito. Por ejemplo, el conjunto N = {1, 2, 3, ...} de los números naturales es infinito. Todo conjunto finito es un conjunto numerable, puesto que sus elementos pueden contarse, pero la recíproca es falsa: existen conjuntos numerables que no son finitos (como el propio N).

Los conjuntos finitos son particularmente importantes en combinatoria.