combinatoria
"Combinatoria"
Combinatoria es una rama de la matemática perteneciente al área de matemáticas discretas que estudia la enumeración, construcción y existencia de propiedades de configuraciones que satisfacen ciertas condiciones establecidas. Además, estudia las ordenaciones o agrupaciones de un determinado número de elementos.
Combinatoria:estudia las ordenaciones o agrupaciones de un determinado número de elementos.En todo problema combinatorio hay varios conceptos claves que debemos distinguir.
Combinatoria:En esta unidad se pretende estudiar técnicas de recuento que permitan conocer el número de elementos de aquellos conjuntos o la forma de realizar agrupaciones con sus elementos, en los que, por la extensión de los mismos, no es posible contar de uno en uno los elementos, pero que poseen algunas propiedades que permiten deducirlo utilizando algún procedimiento o fórmula.
Combinatoria:es la parte de las Matemáticas que estudia las diversas formas de realizar agrupaciones con los elementos de un conjunto, formándolas y calculando su número.
"Permutacion"
En matemáticas, una permutación es la variación del orden o de la disposición de los elementos de un conjunto ordenado o una tupla sin elementos repetidos.


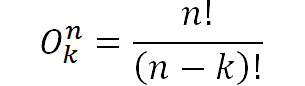

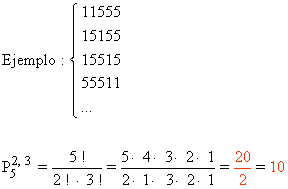

Combinatoria es una rama de la matemática perteneciente al área de matemáticas discretas que estudia la enumeración, construcción y existencia de propiedades de configuraciones que satisfacen ciertas condiciones establecidas. Además, estudia las ordenaciones o agrupaciones de un determinado número de elementos.
Combinatoria:estudia las ordenaciones o agrupaciones de un determinado número de elementos.En todo problema combinatorio hay varios conceptos claves que debemos distinguir.
Combinatoria:En esta unidad se pretende estudiar técnicas de recuento que permitan conocer el número de elementos de aquellos conjuntos o la forma de realizar agrupaciones con sus elementos, en los que, por la extensión de los mismos, no es posible contar de uno en uno los elementos, pero que poseen algunas propiedades que permiten deducirlo utilizando algún procedimiento o fórmula.
Combinatoria:es la parte de las Matemáticas que estudia las diversas formas de realizar agrupaciones con los elementos de un conjunto, formándolas y calculando su número.
"Permutacion"
En matemáticas, una permutación es la variación del orden o de la disposición de los elementos de un conjunto ordenado o una tupla sin elementos repetidos.
Se llama permutación de n elementos a cada una de las diferentes ordenaciones que se pueden hacer con esos elementos. Ejemplo :
{a, b, c} Elementos
"Permutacion con repetición"
Las permutaciones con repetición de elementos en las que el primer elemento se repite veces, el segundo veces, ... y el último se repite veces, son los distintos grupos de elementos que se pueden hacer de forma que en cada grupo, cada elemento aparezca el número de veces indicado. Además, dos grupos se diferencian únicamente en el orden de la colocación. Se representa por .
Permutaciones con repetición de n elementos en las que el primer elemento se repite n1 veces, el segundo se repite n2 veces ... y el último se repite nk veces son los distintos grupos de n elementos que se pueden hacer de forma que en cada grupo, cada elemento aparezca el número de veces indicado y que dos grupos se diferencian únicamente en el orden de colocación. Se representa por Pnn1,n2,...,nk.
"Combinación"
Una combinación es un arreglo donde el orden NO es importante. La notación para las combinaciones es C(n,r) que es la cantidad de combinaciones de “n” elementos seleccionados, “r” a la vez. Es igual a la cantidad de permutaciones de “n” elementos tomados “r” a la vez dividido por “r” factorial. Esto sería P(n,r)/r! en notación matemática
Con origen en el latín combinatio, combinación es una palabra que refiere al acto y consecuencia de combinar algo o de combinarse(es decir, unir, complementar o ensamblar cosas diversas para lograr un compuesto). El concepto posee múltiples aplicaciones ya que las cosas factibles de combinar son de características y orígenes muy diversos.
"Formula de Permutacion"

"Formula de Permutacion con repeticion"

"Formula de combinación"
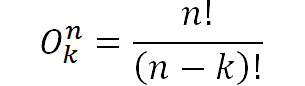
"Ejercicios de permutacion"
1.-¿Cuántos números de 5 cifras diferentes se puede formar con los dígitos: 1, 2, 3, 4, 5.?
m = 5 n = 5
Sí entran todos los elementos. De 5 dígitos entran sólo 3.
Sí importa el orden. Son números distintos el 123, 231, 321.
2.-¿De cuántas formas distintas pueden sentarse ocho personas en una fila de butacas?
Sí entran todos los elementos. Tienen que sentarse las 8 personas.
Sí importa el orden.
3.-Con las cifras 2, 2, 2, 3, 3, 3, 3, 4, 4; ¿cuántos números de nueve cifras se pueden formar?
m = 9 a = 3 b = 4 c = 2 a + b + c = 9
Sí entran todos los elementos.
Sí importa el orden.
Sí se repiten los elementos.
4.-Con las letras de la palabra libro, ¿cuántas ordenaciones distintas se pueden hacer que empiecen por vocal?
La palabra empieza por i u o seguida de las 4 letras restantes tomadas de 4 en 4.
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.
5.-¿Cuántos números de cinco cifras distintas se pueden formar con las cifras impares? ¿Cuántos de ellos son mayores de 70.000?
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.

Si es impar sólo puede empezar por 7 u 8
"Ejercicios de permutacion con repetición"
1.-¿Cuántos números distintos se pueden escribir con los dígitos 1 y 5 en que el 1 se repite
2 veces, el 5 se repite 3 veces?
2 veces, el 5 se repite 3 veces?
- Intervienen todos los elementos.
- Se pueden repetir.
- Influye el orden en el que se coloca.
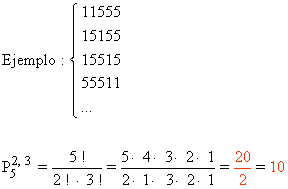
Ejemplo 4:
2.-¿Cuántos números diferentes pueden formarse con las cifras del número 458870?

3.-a.¿Cuántas claves de acceso a una computadora será posible diseñar con los números 1,1,1,2,3,3,3,3?, b.¿cuántas de las claves anteriores empiezan por un número uno seguido de un dos?, c. ¿cuántas de las claves del inciso a empiezan por el número dos y terminan por el número tres?
Solución:
a. n = 8 números
x1 = 3 números uno
x2 = 1 número dos
x3 = 4 números cuatro
8P3,1,4 = 8! / 3!1!4! = 280 claves de acceso
4) ¿De cuántas maneras es posible plantar en una línea divisoria de un terreno dos nogales, cuatro manzanos y tres ciruelos?
Solución:
n = 9 árboles
x1 = 2 nogales
x2 = 4 manzanos
x3 = 3 ciruelos
9P2,4,3 = 9! / 2!4!3! = 1260 maneras de plantar los árboles
5) Si un equipo de fútbol soccer femenil participa en 12 juegos en una temporada, ¿cuántas maneras hay de que entre esos doce juegos en que participa, obtenga 7 victorias, 3 empates y 2 juegos perdidos?
Solución:
n = 12 juegos
x1 = 7 victorias
x2 = 3 empates
x3 = 2 juegos perdidos
12P7,3,2 = 12! / 7!3!2! = 7,920 maneras de que en la temporada este equipo logre siete victorias, tres empates y dos juegos perdidos.
"Ejercicios de combinacion"
1.-En una bodega hay en un cinco tipos diferentes de botellas. ¿De cuántas formas se pueden elegir cuatro botellas?
No entran todos los elementos. Sólo elije 4..
No importa el orden. Da igual que elija 2 botellas de anís y 2 de ron, que 2 de ron y 2 de anís.
Sí se repiten los elementos. Puede elegir más de una botella del mismo tipo.
2.-Un grupo, compuesto por cinco hombres y siete mujeres, forma un comité de 5 hombres y 3 mujeres. De cuántas formas puede formarse, si:
Soluciones:
Puede pertenecer a él cualquier hombre o mujer.
 Una mujer determinada debe pertenecer al comité.
Una mujer determinada debe pertenecer al comité.
 Dos hombres determinados no pueden estar en el comité.
Dos hombres determinados no pueden estar en el comité.
3.-Con parte de su primer salario un chavo decide comprar 3 de los siete discos compactos que le faltan del grupo el tri. ¿Cuántas posibilidades tiene?
Hay que elegir 3 objetos (sin importar el orden) de un conjunto de siete. Hay entonces
Se requiere ahora escoger cuatro objetos de un conjunto de doce. Observemos que se nuevo el orden en que se escogen las ocho preguntas resulta irrelevante, puesto que, por ejemplo , da lo mismo seleccionar las preguntas 4,5,8 y 11 que las preguntas 11,4,5 y 8. El estudiante puede responder este examen de


3.-Con parte de su primer salario un chavo decide comprar 3 de los siete discos compactos que le faltan del grupo el tri. ¿Cuántas posibilidades tiene?
Hay que elegir 3 objetos (sin importar el orden) de un conjunto de siete. Hay entonces
4.-En un examen de Historia se requiere contestar cuatro de doce preguntas. ¿Cuántas maneras diferentes hay de contestar este examen?
Se requiere ahora escoger cuatro objetos de un conjunto de doce. Observemos que se nuevo el orden en que se escogen las ocho preguntas resulta irrelevante, puesto que, por ejemplo , da lo mismo seleccionar las preguntas 4,5,8 y 11 que las preguntas 11,4,5 y 8. El estudiante puede responder este examen de
5.-
La tienda de regalos de un centro turístico tiene quince postales distintas ¿De cuantas maneras puede seleccionar una persona cuatro de estas postales como recuerdo?
N=15 r=4
15C4 = 15!/ 4! (15-4)! = 1365


Comentarios
Publicar un comentario